Parallel Data Transmission

Posted on 02-05-2021 by admin

What Is Meant By Parallel Data Transmission
Application Of Parallel Data Transmission
Serial Data Transmission
Forms Of Data Transmission
Parallel Data Transmission Advantages

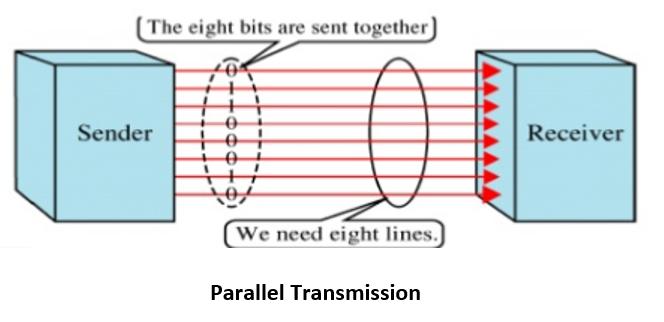
Parallel data transmission In parallel data transmission, multiple bits are sent simultaneously down different wires (channels) within the same cable. Data is synchronised by a clock, however this becomes problematic over longer distances where synchronisation errors may start to occur. In this paper a new parallel data transmission process has been proposed. In this research all segmented data broken in the transport layer at the same time, transfer through the medium. Serial and Parallel Transmission Digital data transmission can occur in two basic modes: serial or parallel. Data within a computer system is transmitted via parallel mode on buses with the width of the parallel bus matched to the word size of the computer system. Data between computer systems is usually transmitted in bit serial mode. Parallel data transmission is used in the internal electronics of the computer system. The pathways between the CPU and the memory all use this method of data transmission. Integrated circuits, buses and other internal components all use parallel data transmission because of the need for high speed data.

A series-parallel partial order, shown as a Hasse diagram.

ARINC 429's data encoding uses a complementary differential bipolar return-to-zero (BPRZ) transmission waveform, further reducing EMI emissions from the cable itself. Development tools edit When developing and/or troubleshooting the ARINC 429 bus, examination of hardware signals can be very important to find problems.

In order-theoretic mathematics, a series-parallel partial order is a partially ordered set built up from smaller series-parallel partial orders by two simple composition operations.^[1]^[2]

The series-parallel partial orders may be characterized as the N-free finite partial orders; they have order dimension at most two.^[1]^[3] They include weak orders and the reachability relationship in directed trees and directed series–parallel graphs.^[2]^[3] The comparability graphs of series-parallel partial orders are cographs.^[2]^[4]

Series-parallel partial orders have been applied in job shop scheduling,^[5]machine learning of event sequencing in time series data,^[6] transmission sequencing of multimedia data,^[7] and throughput maximization in dataflow programming.^[8]

Series-parallel partial orders have also been called multitrees;^[4] however, that name is ambiguous: multitrees also refer to partial orders with no four-element diamond suborder^[9] and to other structures formed from multiple trees.

Definition[edit]

Consider P and Q, two partially ordered sets. The series composition of P and Q, written P; Q,^[7]P * Q,^[2] or P ⧀ Q,^[1]is the partially ordered set whose elements are the disjoint union of the elements of P and Q. In P; Q, two elements x and y that both belong to P or that both belong to Q have the same order relation that they do in P or Q respectively. However, for every pair x, y where x belongs to P and y belongs to Q, there is an additional order relation x ≤ y in the series composition. Series composition is an associative operation: one can write P; Q; R as the series composition of three orders, without ambiguity about how to combine them pairwise, because both of the parenthesizations (P; Q); R and P; (Q; R) describe the same partial order. However, it is not a commutative operation, because switching the roles of P and Q will produce a different partial order that reverses the order relations of pairs with one element in P and one in Q.^[1]

The parallel composition of P and Q, written P || Q,^[7]P + Q,^[2] or P ⊕ Q,^[1] is defined similarly, from the disjoint union of the elements in P and the elements in Q, with pairs of elements that both belong to P or both to Q having the same order as they do in P or Q respectively. In P || Q, a pair x, y is incomparable whenever x belongs to P and y belongs to Q. Parallel composition is both commutative and associative.^[1]

The class of series-parallel partial orders is the set of partial orders that can be built up from single-element partial orders using these two operations. Equivalently, it is the smallest set of partial orders that includes the single-element partial order and is closed under the series and parallel composition operations.^[1]^[2]

A weak order is the series parallel partial order obtained from a sequence of composition operations in which all of the parallel compositions are performed first, and then the results of these compositions are combined using only series compositions.^[2]

Forbidden suborder characterization[edit]

The partial order N with the four elements a, b, c, and d and exactly the three order relations a ≤ b ≥ c ≤ d is an example of a fence or zigzag poset; its Hasse diagram has the shape of the capital letter 'N'. It is not series-parallel, because there is no way of splitting it into the series or parallel composition of two smaller partial orders. A partial order P is said to be N-free if there does not exist a set of four elements in P such that the restriction of P to those elements is order-isomorphic to N. The series-parallel partial orders are exactly the nonempty finite N-free partial orders.^[1]^[2]^[3]

It follows immediately from this (although it can also be proven directly) that any nonempty restriction of a series-parallel partial order is itself a series-parallel partial order.^[1]

Order dimension[edit]

What Is Meant By Parallel Data Transmission

The order dimension of a partial order P is the minimum size of a realizer of P, a set of linear extensions of P with the property that, for every two distinct elements x and y of P, x ≤ y in P if and only if x has an earlier position than y in every linear extension of the realizer. Series-parallel partial orders have order dimension at most two. If P and Q have realizers {L₁, L₂} and {L₃, L₄}, respectively, then {L₁L₃, L₂L₄} is a realizer of the series composition P; Q, and {L₁L₃, L₄L₂} is a realizer of the parallel composition P || Q.^[2]^[3] A partial order is series-parallel if and only if it has a realizer in which one of the two permutations is the identity and the other is a separable permutation.

It is known that a partial order P has order dimension two if and only if there exists a conjugate order Q on the same elements, with the property that any two distinct elements x and y are comparable on exactly one of these two orders. In the case of series parallel partial orders, a conjugate order that is itself series parallel may be obtained by performing a sequence of composition operations in the same order as the ones defining P on the same elements, but performing a series composition for each parallel composition in the decomposition of P and vice versa. More strongly, although a partial order may have many different conjugates, every conjugate of a series parallel partial order must itself be series parallel.^[2]

Connections to graph theory[edit]

Any partial order may be represented (usually in more than one way) by a directed acyclic graph in which there is a path from x to y whenever x and y are elements of the partial order with x ≤ y. The graphs that represent series-parallel partial orders in this way have been called vertex series parallel graphs, and their transitive reductions (the graphs of the covering relations of the partial order) are called minimal vertex series parallel graphs.^[3] Directed trees and (two-terminal) series parallel graphs are examples of minimal vertex series parallel graphs; therefore, series parallel partial orders may be used to represent reachability relations in directed trees and series parallel graphs.^[2]^[3]

The comparability graph of a partial order is the undirected graph with a vertex for each element and an undirected edge for each pair of distinct elements x, y with either x ≤ y or y ≤ x. That is, it is formed from a minimal vertex series parallel graph by forgetting the orientation of each edge. The comparability graph of a series-parallel partial order is a cograph: the series and parallel composition operations of the partial order give rise to operations on the comparability graph that form the disjoint union of two subgraphs or that connect two subgraphs by all possible edges; these two operations are the basic operations from which cographs are defined. Conversely, every cograph is the comparability graph of a series-parallel partial order. If a partial order has a cograph as its comparability graph, then it must be a series-parallel partial order, because every other kind of partial order has an N suborder that would correspond to an induced four-vertex path in its comparability graph, and such paths are forbidden in cographs.^[2]^[4]

Computational complexity[edit]

The forbidden suborder characterization of series-parallel partial orders can be used as a basis for an algorithm that tests whether a given binary relation is a series-parallel partial order, in an amount of time that is linear in the number of related pairs.^[2]^[3] Alternatively, if a partial order is described as the reachability order of a directed acyclic graph, it is possible to test whether it is a series-parallel partial order, and if so compute its transitive closure, in time proportional to the number of vertices and edges in the transitive closure; it remains open whether the time to recognize series-parallel reachability orders can be improved to be linear in the size of the input graph.^[10]

If a series-parallel partial order is represented as an expression tree describing the series and parallel composition operations that formed it, then the elements of the partial order may be represented by the leaves of the expression tree. A comparison between any two elements may be performed algorithmically by searching for the lowest common ancestor of the corresponding two leaves; if that ancestor is a parallel composition, the two elements are incomparable, and otherwise the order of the series composition operands determines the order of the elements. In this way, a series-parallel partial order on n elements may be represented in O(n) space with O(1) time to determine any comparison value.^[2]

It is NP-complete to test, for two given series-parallel partial orders P and Q, whether P contains a restriction isomorphic to Q.^[3]

Although the problem of counting the number of linear extensions of an arbitrary partial order is #P-complete,^[11] it may be solved in polynomial time for series-parallel partial orders. Specifically, if L(P) denotes the number of linear extensions of a partial order P, then L(P; Q) = L(P)L(Q) and

{displaystyle L(P||Q)={frac {(|P|+|Q|)!}{|P|!|Q|!}}L(P)L(Q),}

so the number of linear extensions may be calculated using an expression tree with the same form as the decomposition tree of the given series-parallel order.^[2]

Applications[edit]

Mannila & Meek (2000) use series-parallel partial orders as a model for the sequences of events in time series data. They describe machine learning algorithms for inferring models of this type, and demonstrate its effectiveness at inferring course prerequisites from student enrollment data and at modeling web browser usage patterns.^[6]

Amer et al. (1994) argue that series-parallel partial orders are a good fit for modeling the transmission sequencing requirements of multimedia presentations. They use the formula for computing the number of linear extensions of a series-parallel partial order as the basis for analyzing multimedia transmission algorithms.^[7]

Choudhary et al. (1994) use series-parallel partial orders to model the task dependencies in a dataflow model of massive data processing for computer vision. They show that, by using series-parallel orders for this problem, it is possible to efficiently construct an optimized schedule that assigns different tasks to different processors of a parallel computing system in order to optimize the throughput of the system.^[8]

A class of orderings somewhat more general than series-parallel partial orders is provided by PQ trees, data structures that have been applied in algorithms for testing whether a graph is planar and recognizing interval graphs.^[12] A P node of a PQ tree allows all possible orderings of its children, like a parallel composition of partial orders, while a Q node requires the children to occur in a fixed linear ordering, like a series composition of partial orders. However, unlike series-parallel partial orders, PQ trees allow the linear ordering of any Q node to be reversed.

References[edit]

^ ^a^b^c^d^e^f^g^hⁱBechet, Denis; De Groote, Philippe; Retoré, Christian (1997), 'A complete axiomatisation for the inclusion of series-parallel partial orders', Rewriting Techniques and Applications, Lecture Notes in Computer Science, 1232, Springer-Verlag, pp. 230–240, doi:10.1007/3-540-62950-5_74.
^ ^a^b^c^d^e^f^g^hⁱ^j^k^l^mⁿ^oMöhring, Rolf H. (1989), 'Computationally tractable classes of ordered sets', in Rival, Ivan (ed.), Algorithms and Order: Proceedings of the NATO Advanced Study Institute on Algorithms and Order, Ottawa, Canada, May 31-June 13, 1987, NATO Science Series C, 255, Springer-Verlag, pp. 105–194, ISBN978-0-7923-0007-6.
^ ^a^b^c^d^e^f^g^hValdes, Jacobo; Tarjan, Robert E.; Lawler, Eugene L. (1982), 'The recognition of series parallel digraphs', SIAM Journal on Computing, 11 (2): 298–313, doi:10.1137/0211023.
^ ^a^b^cJung, H. A. (1978), 'On a class of posets and the corresponding comparability graphs', Journal of Combinatorial Theory, Series B, 24 (2): 125–133, doi:10.1016/0095-8956(78)90013-8, MR0491356.
^Lawler, Eugene L. (1978), 'Sequencing jobs to minimize total weighted completion time subject to precedence constraints', Annals of Discrete Mathematics, 2: 75–90, doi:10.1016/S0167-5060(08)70323-6, ISBN9780720410433, MR0495156CS1 maint: discouraged parameter (link).
^ ^a^bMannila, Heikki; Meek, Christopher (2000), 'Global partial orders from sequential data', Proc. 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2000), pp. 161–168, doi:10.1145/347090.347122, S2CID14735932.
^ ^a^b^c^dAmer, Paul D.; Chassot, Christophe; Connolly, Thomas J.; Diaz, Michel; Conrad, Phillip (1994), 'Partial-order transport service for multimedia and other applications', IEEE/ACM Transactions on Networking, 2 (5): 440–456, doi:10.1109/90.336326, S2CID1974607.
^ ^a^bChoudhary, A. N.; Narahari, B.; Nicol, D. M.; Simha, R. (1994), 'Optimal processor assignment for a class of pipelined computations', IEEE Transactions on Parallel and Distributed Systems, 5 (4): 439–445, doi:10.1109/71.273050.
^Furnas, George W.; Zacks, Jeff (1994), 'Multitrees: enriching and reusing hierarchical structure', Proc. SIGCHI conference on Human Factors in Computing Systems (CHI '94), pp. 330–336, doi:10.1145/191666.191778, S2CID18710118.
^Ma, Tze-Heng; Spinrad, Jeremy (1991), 'Transitive closure for restricted classes of partial orders', Order, 8 (2): 175–183, doi:10.1007/BF00383402, S2CID120935610.
^Brightwell, Graham R.; Winkler, Peter (1991), 'Counting linear extensions', Order, 8 (3): 225–242, doi:10.1007/BF00383444, S2CID119697949.
^Booth, Kellogg S.; Lueker, George S. (1976), 'Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms', Journal of Computer and System Sciences, 13 (3): 335–379, doi:10.1016/S0022-0000(76)80045-1.

Retrieved from 'https://en.wikipedia.org/w/index.php?title=Series-parallel_partial_order&oldid=1016713398'

ARINC 429,^[1] 'Mark33 Digital Information Transfer System (DITS),' is also known as the Aeronautical Radio INC. (ARINC) technical standard for the predominant avionicsdata bus used on most higher-end commercial and transport aircraft.^[2] It defines the physical and electrical interfaces of a two-wire data bus and a data protocol to support an aircraft's avionics local area network.

Technical description[edit]

Medium and Signaling[edit]

Application Of Parallel Data Transmission

ARINC 429 is a data transfer standard for aircraft avionics. It uses a self-clocking, self-synchronizing data bus protocol (Tx and Rx are on separate ports). The physical connection wires are twisted pairs carrying balanced differential signaling. Data words are 32 bits in length and most messages consist of a single data word. Messages are transmitted at either 12.5 or 100 kbit/s^[3] to other system elements that are monitoring the bus messages. The transmitter constantly transmits either 32-bit data words or the NULL state (0 Volts). A single wire pair is limited to one transmitter and no more than 20 receivers. The protocol allows for self-clocking at the receiver end, thus eliminating the need to transmit clocking data. ARINC 429 is an alternative to MIL-STD-1553.

Bit numbering, Transmission Order, and Bit Significance[edit]

The ARINC 429 unit of transmission is a fixed-length 32-bit frame, which the standard refers to as a 'word'. The bits within an ARINC 429 word are serially identified from Bit Number 1 to Bit Number 32^[4] or simply Bit 1 to Bit 32. The fields and data structures of the ARINC 429 word are defined in terms of this numbering.

While it is common to illustrate serial protocol frames progressing in time from right to left, a reversed ordering is commonly practiced within the ARINC standard. Even though ARINC 429 word transmission begins with Bit 1 and ends with Bit 32, it is common to diagram^[5] and describe^[6]^[7] ARINC 429 words in the order from Bit 32 to Bit 1. In simplest terms, while the transmission order of bits (from the first transmitted bit to the last transmitted bit) for a 32-bit frame is conventionally diagrammed as

First bit > 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, .. 29, 30, 31, 32 < Last bit,

Everspace™ - upgrade to deluxe edition for mac. this sequence is often diagrammed in ARINC 429 publications in the opposite direction as

Last bit > 32, 31, 30, 29, .. 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 < First bit.

When the ARINC 429 word format is illustrated with Bit 32 to the left, the numeric representations in the data field generally read with the Most significant bit on the left. However, in this particular bit order presentation, the Label field reads with its most significant bit on the right. Like CAN Protocol Identifier Fields,^[8] ARINC 429 label fields are transmitted most significant bit first. However, like UART Protocol, Binary-coded decimal numbers and binary numbers in the ARINC 429 data fields are generally transmitted least significant bit first.

Serial Data Transmission

Some equipment suppliers^[9]^[10] publish the bit transmission order as

First bit > 8, 7, 6, 5, 4, 3, 2, 1, 9, 10, 11, 12, 13 … 32 < Last bit.

The suppliers that use this representation have in effect renumbered the bits in the Label field, converting the standard’s MSB 1 bit numbering for that field to LSB 1 bit numbering. This renumbering highlights the relative reversal of 'bit endianness' between the Label representation and numeric data representations as defined within the ARINC 429 standard. Of note is how the 87654321 bit numbering is similar to the 76543210bit numbering common in digital equipment; but reversed from the 12345678 bit numbering defined for the ARINC 429 Label field.

This notional reversal also reflects historical implementation details. ARINC 429 transceivers have been implemented with 32-bit shift registers.^[11] Parallel access to that shift register is often octet-oriented. As such, the bit order of the octet access is the bit order of the accessing device, which is usually LSB 0; and serial transmission is arranged such that the least significant bit of each octet is transmitted first. So, in common practice, the accessing device wrote or read a 'reversed label'^[12] (for example, to transmit a Label 213₈ [or 8B₁₆] the bit-reversed value D1₁₆ is written to the Label octet). Newer or 'enhanced' transceivers may be configured to reverse the Label field bit order 'in hardware.'^[13]

Word format[edit]

ARINC 429 Word Format
P	SSM		MSB				Data											LSB				SDI		LSB		Label				MSB
32	31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1

Each ARINC 429 word is a 32-bit sequence that contains five fields:

Bit 32 is the parity bit, and is used to verify that the word was not damaged or garbled during transmission. Every ARINC 429 channel typically uses 'odd' parity - there must be an odd number of '1' bits in the word. This bit is set to 0 or 1 to ensure that the correct number of bits are set to 1 in the word.

Bits 30 to 31 are the Sign/Status Matrix (SSM) - these bits may have various encodings dependent on the particular data representation applied to a given word:

In all cases using the SSM, these bits may be encoded to indicate:

Normal Operation (NO) - Indicates the data in this word is considered to be correct data.

Functional Test (FT) - Indicates that the data is being provided by a test source.

Failure Warning (FW) - Indicates a failure which causes the data to be suspect or missing.

No Computed Data (NCD) - Indicates that the data is missing or inaccurate for some reason other than a failure. For example, autopilot commands will show as NCD when the autopilot is not turned on.

In the case of Binary Coded Decimal (BCD) representation, the SSM may also indicate the Sign (+/-) of the data or some information analogous to sign, like an orientation (North/South; East/West). When so indicating sign, the SSM is also considered to be indicating Normal Operation.
In the case of two's-complement representation of signed binary numbers (BNR), Bit 29 represents the number's sign; that is, sign indication is delegated to Bit 29 in this case.
In the case of discrete data representation (e.g., bit-fields), the SSM has a different, signless encoding.^[14]

SSM		Data Dependent SSM Encodings:
Bit 31	Bit 30	Sign/Status Matrix for BCD Data	Status Matrix for BNR Data	Status Matrix for Discrete Data
0	0	Plus, North, East, Right, To, Above	Failure Warning (FW)	Verified Data, Normal Operation
0	1	No Computed Data (NCD)	No Computed Data (NCD)	No Computed Data (NCD)
1	0	Functional Test (FT)	Functional Test (FT)	Functional Test (FT)
1	1	Minus, South, West, Left, From, Below	Normal Operation (NO)	Failure Warning (FW)

Bit 29	Sign Matrix for BNR Data
0	Plus, North, East, Right, To, Above
1	Minus, South, West, Left, From, Below

Bits 11 to 29 contain the data. Bit-field discrete data, Binary Coded Decimal (BCD), and Binary Number Representation (BNR) are common ARINC 429 data formats. Data formats may also be mixed.

Forms Of Data Transmission

Bits 9 and 10 are Source/Destination Identifiers (SDI) and may indicate the intended receiver or, more frequently, indicate the transmitting subsystem.

Bits 1 to 8 contain a label (label words), expressed in octal (MSB 1 bit numbering), identifying the data type.

The image below exemplifies many of the concepts explained in the adjacent sections. In this image the Label (260) appears in red, the Data in blue-green and the Parity bit in navy blue.

Example ARINC 429
P	SSM		MSB				Data											LSB				SDI		LSB		Label				MSB
32	31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1
1	0	0	1	0	0	0	1	1	0	0	0	1	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	1	0	1
1	0		2		3				3					17								0		0			6			2
JOUR(1)		JOUR(0)				MOIS					Milliseconds

Labels[edit]

Illustration of the airspeed indication and detection system on fly-by-wire aircraft

Label guidelines are provided as part of the ARINC 429 specification, for various equipment types. Each aircraft will contain a number of different systems, such as flight management computers, inertial reference systems, air data computers, radar altimeters, radios, and GPS sensors. For each type of equipment, a set of standard parameters is defined, which is common across all manufacturers and models. For example, any air data computer will provide the barometric altitude of the aircraft as label 203. This allows some degree of interchangeability of parts, as all air data computers behave, for the most part, in the same way. There are only a limited number of labels, though, and so label 203 may have some completely different meaning if sent by a GPS sensor, for example. Very commonly needed aircraft parameters, however, use the same label regardless of source. Also, as with any specification, each manufacturer has slight differences from the formal specification, such as by providing extra data above and beyond the specification, leaving out some data recommended by the specification, or other various changes.

Protection from interference[edit]

Avionics systems must meet environmental requirements, usually stated as RTCA DO-160 environmental categories. ARINC 429 employs several physical, electrical, and protocol techniques to minimize electromagnetic interference with on-board radios and other equipment, for example via other transmission cables.

Its cabling is a shielded 70 Ω twisted-pair.^[1] ARINC signalling defines a 20 Vp differential between the Data A and Data B levels within the bipolar transmission (i.e. 10 V on Data A and -10 V on Data B would constitute a valid driving signal), and the specification defines acceptable voltage rise and fall times.

ARINC 429's data encoding uses a complementary differential bipolar return-to-zero (BPRZ) transmission waveform, further reducing EMI emissions from the cable itself.

Development tools[edit]

When developing and/or troubleshooting the ARINC 429 bus, examination of hardware signals can be very important to find problems. A protocol analyzer is useful to collect, analyze, decode and store signals.